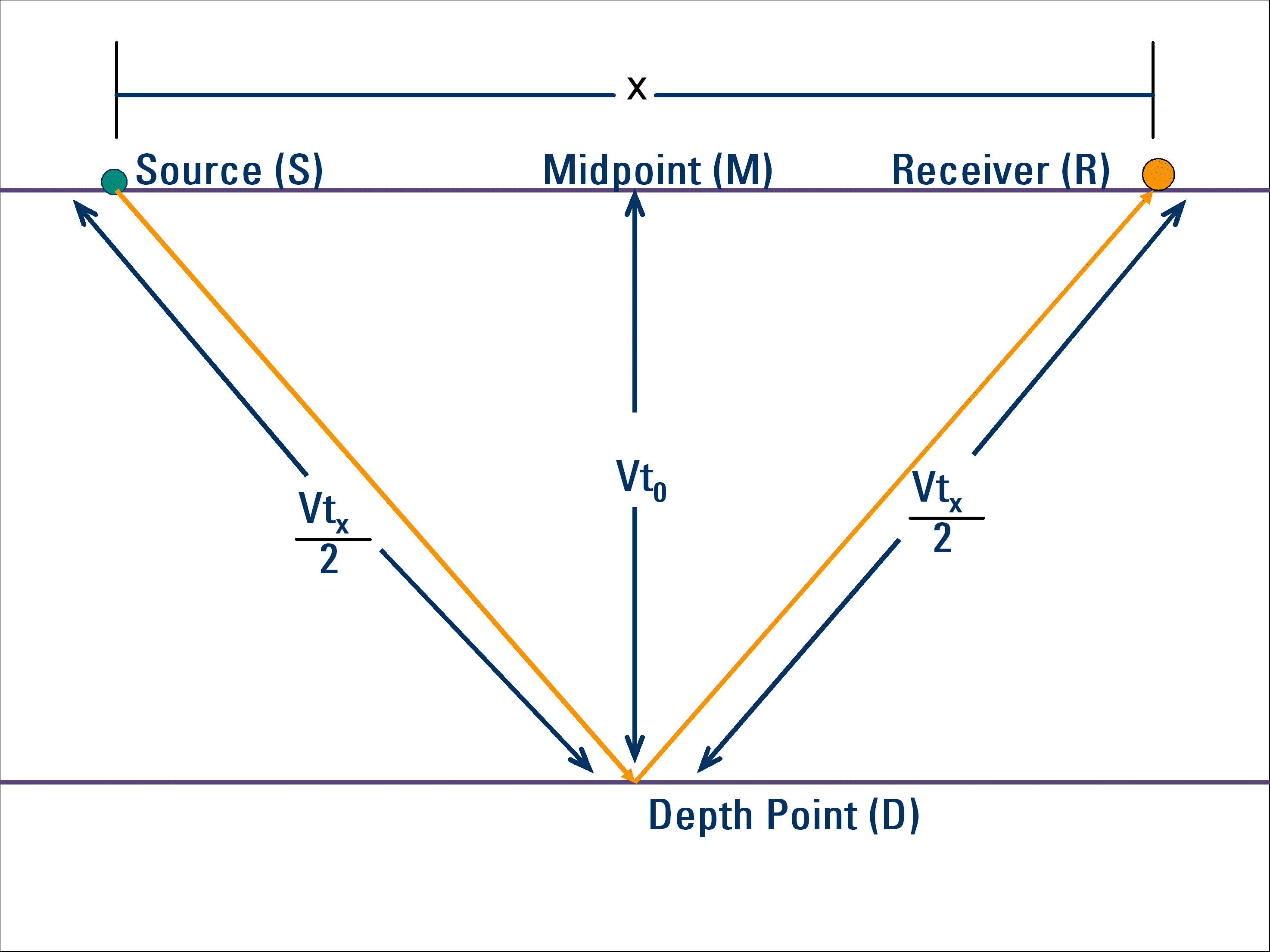
NMO, or normal moveout, is the difference between the zero offset travel time and the travel time observed for a given source-receiver offset in a surface seismic survey. Offset traces must be corrected for normal moveout to correctly position the reflection in time. Figure 2 below shows a single homogenous layer and a single offset source and receiver. The source produces an acoustic wave that travels down through the layer and is reflected back to the receiver with the reflection occurring at the depth point D directly below the midpoint between the source and receiver.

Figure 2 Normal moveout
The normal moveout is then given by :
tNMO = tx � t0. Equation 3
The product of the velocity and the vertical travel time, or VT0 gives the vertical distance from the surface to the depth point D. Similarly the distance traveled by wave from the source to the reflection point D and then the receiver is the product of the velocity and the time that it took for the wave to travel that path VTx. Using the Pythagorean theorem the two distances can be related by the equation:
V2tx2 = V2t02 + x2. Equation 4
Travel time as a function of offset can then be expressed as:
tx2 = t02 + x2/ V2 Equation 5
Note that this is the equation for a hyperbola and that the reflections observed in a common midpoint gather have this shape. By using this equation to substitute for Tx in equation 1 the normal moveout can be obtained:
tNMO = (t02 + x2/ V2)1/2 � t0. Equation 6
To find the velocity, Equation 3 can be rewritten as:
V = [x2 / (tx2 - t02 )]1/2 Equation 7
It can be seen from equation 5 that the NMO velocity can be determined by picking the zero offset travel time, an offset travel time from a CMP gather as illustrated in the figure below and substituting the values and the offset into equation 5.
Once the velocity is obtained the NMO corrections may be calculated. Note that the velocity for a layer may vary laterally so that computations will be made at many points within a seismic survey.